Causal Inference with `group_by` and `summarise`

Lucy D’Agostino McGowan

Wake Forest University

Observational Studies

Goal: To answer a research question

Observational Studies

Goal: To answer a research question

Observational Studies

Randomized Controlled Trial

Observational Studies

Randomized Controlled Trial

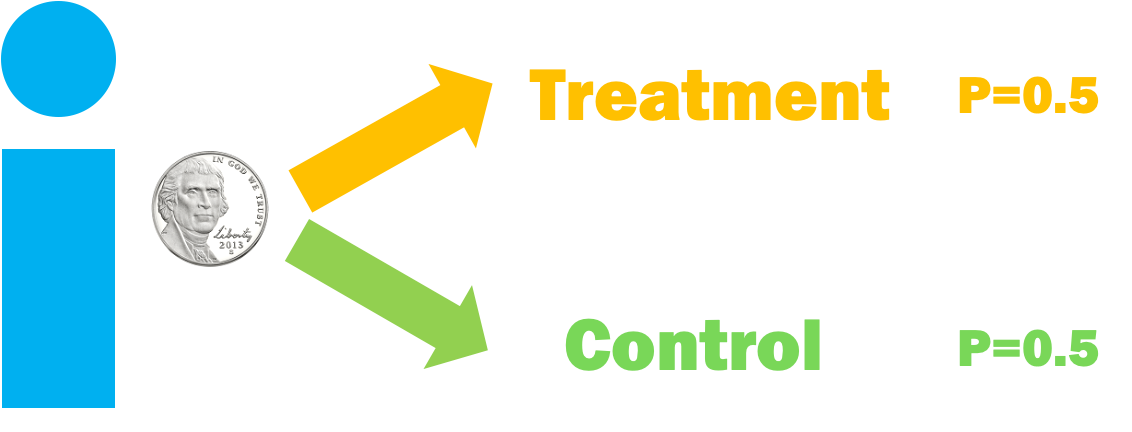
Observational Studies

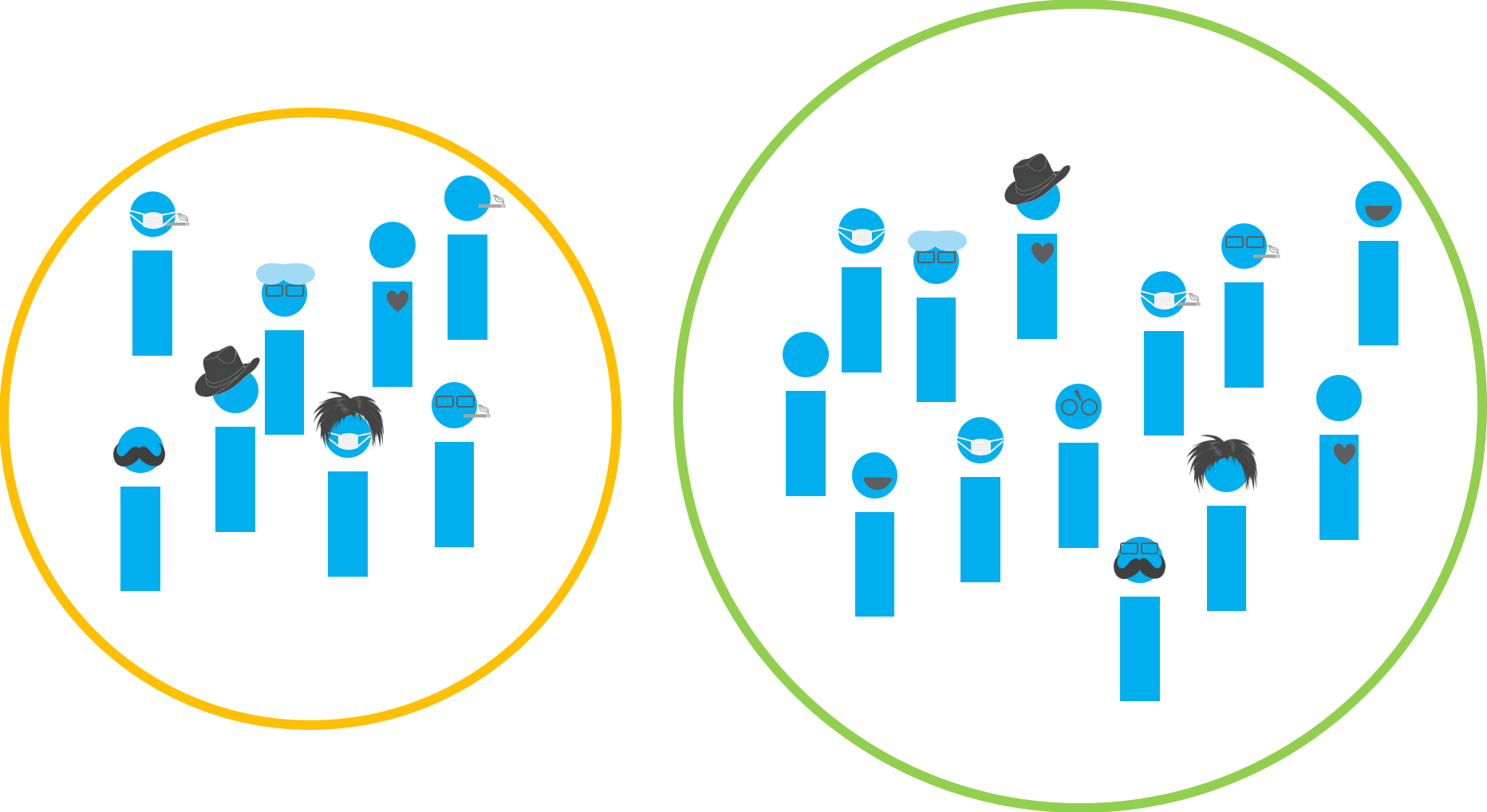
Confounding

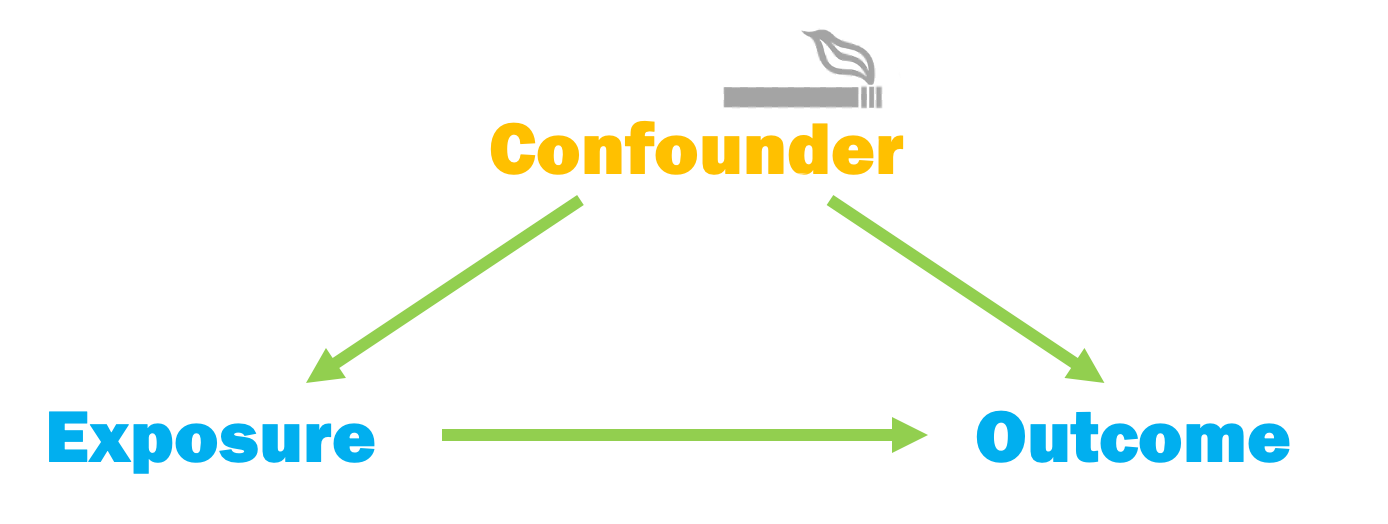
One binary confounder

Simulation

n <- 1000 
sim <- tibble(
  confounder = rbinom(n, 1, 0.5),
  p_exposure = case_when(
    confounder == 1 ~ 0.75,
    confounder == 0 ~ 0.25
  ),
  exposure = rbinom(n, 1, p_exposure),
  outcome = confounder + rnorm(n)
) |> select(-p_exposure)

sim

Simulation

# A tibble: 1,000 × 3
   confounder exposure outcome
        <int>    <int>   <dbl>
 1          0        0  1.13  
 2          0        0  1.11  
 3          1        1  0.129 
 4          1        0  1.21  
 5          0        0  0.0694
 6          1        1 -0.663 
 7          1        1  1.81  
 8          1        1 -0.912 
 9          1        0 -0.247 
10          0        0  0.998 
# ℹ 990 more rows

Simulation

lm(outcome ~ exposure, data = sim)


Call:
lm(formula = outcome ~ exposure, data = sim)

Coefficients:
(Intercept)     exposure  
     0.2688       0.4070

Simulation

sim |>
  group_by(exposure) |>
  summarise(avg_y = mean(outcome))

# A tibble: 2 × 2
  exposure avg_y
     <int> <dbl>
1        0 0.269
2        1 0.676

Simulation

sim |>
  group_by(exposure) |>
  summarise(avg_y = mean(outcome)) |>
  pivot_wider(
    names_from = exposure, 
    values_from = avg_y,  
    names_prefix = "x_"
  ) |>
  summarise(estimate = x_1 - x_0)

# A tibble: 1 × 1
  estimate
     <dbl>
1    0.407

Your Turn 1 (`03-ci-with-group-by-and-summarise-exercises.qmd`)

Group the dataset by `confounder` and `exposure`

Calculate the mean of the `outcome` for the groups

03:00

Your Turn 1

sim |>
  group_by(confounder, exposure) |>
  summarise(avg_y = mean(outcome))

# A tibble: 4 × 3
# Groups:   confounder [2]
  confounder exposure    avg_y
       <int>    <int>    <dbl>
1          0        0 -0.00907
2          0        1 -0.0166 
3          1        0  1.09   
4          1        1  0.936

Your Turn 1

sim |>
  group_by(confounder, exposure) |>
  summarise(avg_y = mean(outcome)) |>
  pivot_wider(
    names_from = exposure,
    values_from = avg_y,  
    names_prefix = "x_"
  ) |>
  summarise(estimate = x_1 - x_0) |>
  # note: we would need to weight this 
  # if the confounder groups were not equal sized
  summarise(estimate = mean(estimate))

# A tibble: 1 × 1
  estimate
     <dbl>
1  -0.0794

🎉

Two binary confounders

Simulation

n <- 1000
sim2 <- tibble(
  confounder_1 = rbinom(n, 1, 0.5),
  confounder_2 = rbinom(n, 1, 0.5), 
  p_exposure = case_when(
    confounder_1 == 1 & confounder_2 == 1 ~ 0.75,
    confounder_1 == 0 & confounder_2 == 1 ~ 0.9,
    confounder_1 == 1 & confounder_2 == 0 ~ 0.2,
    confounder_1 == 0 & confounder_2 == 0 ~ 0.1,
  ),
  exposure = rbinom(n, 1, p_exposure),
  outcome = confounder_1 + confounder_2 + rnorm(n) 
) |> select(-p_exposure)

sim2

Simulation

# A tibble: 1,000 × 4
   confounder_1 confounder_2 exposure outcome
          <int>        <int>    <int>   <dbl>
 1            0            0        0   0.521
 2            1            0        0   1.38 
 3            0            0        0  -0.624
 4            0            1        1   0.427
 5            1            0        1   1.31 
 6            0            0        0  -0.707
 7            1            1        1   2.52 
 8            1            0        0   1.45 
 9            0            0        0  -0.505
10            0            1        1   0.793
# ℹ 990 more rows

Simulation

lm(outcome ~ exposure, data = sim2)


Call:
lm(formula = outcome ~ exposure, data = sim2)

Coefficients:
(Intercept)     exposure  
     0.6395       0.6951

Your Turn 2

Group the dataset by the confounders and exposure

Calculate the mean of the outcome for the groups

02:00

Your Turn 2

sim2 |>
  group_by(confounder_1, confounder_2, exposure) |>
  summarise(avg_y = mean(outcome)) |>
  pivot_wider(
    names_from = exposure,
    values_from = avg_y,  
    names_prefix = "x_"
  ) |>
  summarise(estimate = x_1 - x_0, .groups = "drop") |>
  summarise(estimate = mean(estimate))

# A tibble: 1 × 1
  estimate
     <dbl>
1  -0.0731

Simulation

n <- 100000
big_sim2 <- tibble(
  confounder_1 = rbinom(n, 1, 0.5),
  confounder_2 = rbinom(n, 1, 0.5), 
  p_exposure = case_when(
    confounder_1 == 1 & confounder_2 == 1 ~ 0.75,
    confounder_1 == 0 & confounder_2 == 1 ~ 0.9,
    confounder_1 == 1 & confounder_2 == 0 ~ 0.2,
    confounder_1 == 0 & confounder_2 == 0 ~ 0.1,
  ),
  exposure = rbinom(n, 1, p_exposure),
  outcome = confounder_1 + confounder_2 + rnorm(n) 
) |> select(-p_exposure)

big_sim2

Simulation

# A tibble: 100,000 × 4
   confounder_1 confounder_2 exposure outcome
          <int>        <int>    <int>   <dbl>
 1            1            1        1   2.35 
 2            1            1        0   3.71 
 3            0            0        0   2.08 
 4            0            1        1   0.516
 5            0            0        0  -0.166
 6            1            1        1   1.58 
 7            0            0        0   0.472
 8            1            0        0   3.22 
 9            0            1        1   0.929
10            0            1        1   1.41 
# ℹ 99,990 more rows

Simulation

lm(outcome ~ exposure, data = big_sim2)


Call:
lm(formula = outcome ~ exposure, data = big_sim2)

Coefficients:
(Intercept)     exposure  
     0.6782       0.6561

Simulation

big_sim2 |>
  group_by(confounder_1, confounder_2, exposure) |>
  summarise(avg_y = mean(outcome)) |>
  pivot_wider(
    names_from = exposure,
    values_from = avg_y,  
    names_prefix = "x_"
  ) |>
  summarise(estimate = x_1 - x_0, .groups = "drop") |>
  summarise(estimate = mean(estimate))

# A tibble: 1 × 1
  estimate
     <dbl>
1   0.0187

Continuous confounder?

Simulation

n <- 10000 
sim3 <- tibble(
  confounder = rnorm(n), 
  p_exposure = exp(confounder) / (1 + exp(confounder)),
  exposure = rbinom(n, 1, p_exposure),
  outcome = confounder + rnorm(n) 
) |> select(-p_exposure)

sim3

Simulation

# A tibble: 10,000 × 3
   confounder exposure outcome
        <dbl>    <int>   <dbl>
 1     -0.167        0  -0.560
 2      0.252        1   0.628
 3     -0.321        1  -0.608
 4      0.621        0   1.58 
 5     -0.619        1   0.358
 6     -0.897        0  -1.95 
 7     -2.01         0  -2.50 
 8      0.296        0  -1.10 
 9     -0.504        1  -0.316
10     -0.536        1   1.12 
# ℹ 9,990 more rows

Simulation

lm(outcome ~ exposure, data = sim3)


Call:
lm(formula = outcome ~ exposure, data = sim3)

Coefficients:
(Intercept)     exposure  
    -0.4036       0.8152

Your Turn 3

Use `ntile()` from dplyr to calculate a binned version of `confounder` called `confounder_q`. We’ll create a variable with 5 bins.

Group the dataset by the binned variable you just created and exposure

Calculate the mean of the outcome for the groups

03:00

Your Turn 3

sim3 |>
  mutate(confounder_q = ntile(confounder, 5)) |>
  group_by(confounder_q, exposure) |>
  summarise(avg_y = mean(outcome)) |>
  pivot_wider(
    names_from = exposure,
    values_from = avg_y,  
    names_prefix = "x_"
  ) |>
  summarise(estimate = x_1 - x_0) |>
  summarise(estimate = mean(estimate))

# A tibble: 1 × 1
  estimate
     <dbl>
1   0.0728

Causal Inference with group_by and summarise

Observational Studies

Observational Studies

Observational Studies

Randomized Controlled Trial

Observational Studies

Randomized Controlled Trial

Observational Studies

Confounding

Confounding

One binary confounder

Simulation

Simulation

Simulation

Simulation

Simulation

Your Turn 1 (03-ci-with-group-by-and-summarise-exercises.qmd)

Group the dataset by confounder and exposure

Calculate the mean of the outcome for the groups

Your Turn 1

Your Turn 1

Two binary confounders

Simulation

Simulation

Simulation

Your Turn 2

Group the dataset by the confounders and exposure

Calculate the mean of the outcome for the groups

Your Turn 2

Simulation

Simulation

Simulation

Simulation

Continuous confounder?

Simulation

Simulation

Simulation

Your Turn 3

Use ntile() from dplyr to calculate a binned version of confounder called confounder_q. We’ll create a variable with 5 bins.

Group the dataset by the binned variable you just created and exposure

Calculate the mean of the outcome for the groups

Your Turn 3

What if we could come up with a summary score of all confounders?

Causal Inference with `group_by` and `summarise`

Your Turn 1 (`03-ci-with-group-by-and-summarise-exercises.qmd`)

Group the dataset by `confounder` and `exposure`

Calculate the mean of the `outcome` for the groups

Use `ntile()` from dplyr to calculate a binned version of `confounder` called `confounder_q`. We’ll create a variable with 5 bins.